Question

Hi, can you help me answer this question please, thank you!

Answer 1

Given data:

Coke

Population SD (σ₁) = 0.073

Sample size (n₁) = 48

Sample Mean (x₁) = 12.01 ounces

Pepsi

Population SD (σ₂) = 0.068

Sample Size (n₂) = 46 cans

Sample Mean (x₂) = 12 ounces

Find: test statistic value and p-value

Solution:

Since the sample size is large for both populations (sample size > 30), we shall use the z-statistic for two samples. The formula is:

`z=\frac{\bar{x}_1-\bar{x}_2}{\sqrt[]{(\sigma^2_1)/(n_1)+(\sigma^2_2)/(n_2)}}`

Having those given data, let's plug it in to the formula we have.

`z=\frac{12.01-12}{\sqrt[]{(0.073^2)/(48)+(0.068^2)/(46)}}`
`z=(0.01)/(0.0145445)\approx0.688`

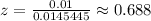
Hence, the test statistic z = 0.688.

The p-value equivalent of this test statistic is 0.4917.