Answer
The second car will catch up to the first car after 8/9th of an hour
SOLUTION
Problem Statement
The question tells us a car leaves a town with a speed of 40km/hr and we are required to find how long it will take a second car that begun the same journey an hour after, moving at 85km/hr to catch the first car.
Method
To solve this question, we only require two things:
1. Sound logical reasoning.
2. Formula for Distance calculation.
The formula is:
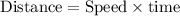
Solution
Before we proceed to solve, we need to understand the question very well. The question says that car 2 catches up with car 1 after some time. This also implies that both car 1 and car 2 would have traveled the exact same distance when car 2 catches up with car 1.
This, therefore, means that if we can find the expression for the distance traveled by both cars, we can equate them.
This leads us to our first step for the solution.
Step 1: Working with the distance
Let us assume that the first car has moved a total of X kilometers after time t1, when the second car catches up to it.
This means that the distance covered by the first car can be written using the formula given above:

Similarly, we can find an expression for the distance moved by the second car as follows:
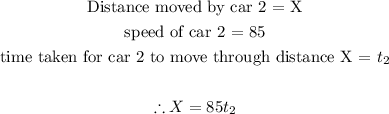
Since the two expressions are the expressions for the same distance covered by both cars after times t1 and t2 respectively, then we can equate them together and find an expression relating t1 to t2. This is shown below:
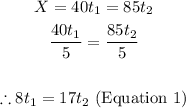
Step 2: Working with the time
Also, we are told that the second car takes off 1 hour after the first car. We can also deduce that the time taken for car 2 to meet up with car 1, is 1 hour less. This means that t2 is less than t1 by 1 hour.
Thus, we can write:
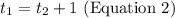
Step 3: Solving both equations simultaneously
Now that we have the two equations in terms t1 and t2, we can proceed to solve them simultaneously.
We shall take Equation 2 and substitute it into Equation 1.

Final answer
Thus, the second car will catch up to the first car after 8/9th of an hour