Question

Can somebody please walk me through this assignment? I don’t understand how to do it

Answer 1

Given

`y=ax^3+bx^2+cx+d`

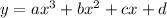
and the data points

x feet y deflection

0 0

1 116

2 448

3 972

substituting the data points, (x, y)

(0, 0) -> 0 = 0 + 0 + 0 + d

=> d = 0.

`\begin{gathered} (1,116)\Rightarrow116=a+b+c \\ (2,448)\Rightarrow448=8a+4b+2c \\ (3,972)\Rightarrow972=27a+9b+3c \end{gathered}`
`\begin{gathered} \begin{bmatrix}{1} & {1} & {1} \\ {8} & {4} & {2} \\ {27} & {9} & {3}\end{bmatrix}\begin{bmatrix}{a} & {} & {} \\ {b} & {} & {} \\ {c} & {} & {}\end{bmatrix}=\begin{bmatrix}{116} & {} & {} \\ {448} & {} & {} \\ {972} & {} & {}\end{bmatrix} \\ \end{gathered}`

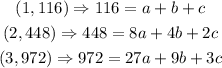
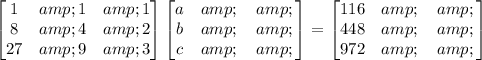
Using crammer's rule,

D = 1(12 - 18) - 1(24 - 54) + 1(72 - 108) = -12

`\begin{gathered} a=\frac{\det \begin{bmatrix}{116} & {1} & {1} \\ {448} & {4} & {2} \\ {972} & {9} & {3}\end{bmatrix}}{\det \begin{bmatrix}{1} & {1} & {1} \\ {8} & {4} & {2} \\ {27} & {9} & {3}\end{bmatrix}}=(116(12-18)-1(1344-1944)+1(4032-3888))/(-12)=-4 \\ b=\frac{\det \begin{bmatrix}{1} & {116} & {1} \\ {8} & {448} & {2} \\ {27} & {972} & {3}\end{bmatrix}}{\det \begin{bmatrix}{1} & {1} & {1} \\ {8} & {4} & {2} \\ {27} & {9} & {3}\end{bmatrix}}=(1(1344-1944)-116(24-54)+1(4032-3888))/(-12)=120 \\ c=\frac{\det \begin{bmatrix}{1} & {1} & {116} \\ {8} & {4} & {448} \\ {27} & {9} & {972}\end{bmatrix}}{\det \begin{bmatrix}{1} & {1} & {1} \\ {8} & {4} & {2} \\ {27} & {9} & {3}\end{bmatrix}}=(1(3888-4032)-(7776-12096)+116(72-108))/(-12)=0 \end{gathered}`

Hence, a = -4, b = 120 and c = 0

Hence, the particular function that models this data is;

`f(x)=-4x^3+120x^2`

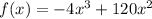
Looking at the particular function, d = 0

(b)

`f(x)=x^2(-4x+120)^{}`

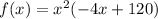
Hence, the multiplicity of 0 is 2

(c) When x = 8

`f(8)=-4(8)^3+120(8)^2=5632`

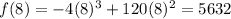
(d)