Although she is not credit overloaded, the savings shouldn't be counted as spent.
Thus, the total spent, in dollars, is given by:
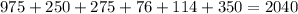
Notice that we added all the items except for the savings.
Thus, she is not credit overloaded because she spends $2040 and receives $2255 every month.