We have to solve this system of linear equations.
As we have the same coefficient for y, the most effective method to solve this is by elimination: we substract the first equation from the second one and then solve for x, as y is no longer part of this new equation.
We then substract the equations:
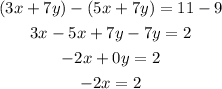
Then, we can solve for x:
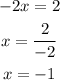
Then, we can pick any of the two equations and, with the value of x = -1, we can solve for y as:
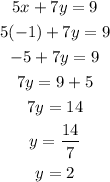
Answer: x = -1 and y = 2.