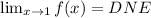1 Answer

Korpel · Answer 1 · 2024-01-02T06:00:17+0000

The function f is given by:

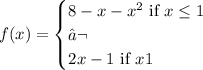
$f(x)=\begin{cases}{8-x-x^2\text{ if }x\leq1} \\ {\placeholder{⬚}} \\ 2x-1\text{ if }x\gt1\end{cases}$

Therefore,

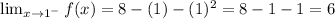
$\lim_(x\to1^-)f(x)=8-(1)-(1)^2=8-1-1=6$

Therefore,

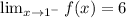
$\lim_(x\to1^-)f(x)=6$

Hence, the limit of f(x) as x tends to 1 from the left is 6

$\begin{gathered} \lim_(x\to1^+)f(x)=2(1)-1=1 \\ \operatorname{\lim}_(x\to1^+)f(x)=1 \end{gathered}$

Hence, the limit of f(x) as x tends to 1 from the right is 1

Since the left limit is not equal to the right limit, it follows that the limit of f(x) as x tends to 1 does not exist:

$\lim_(x\to1)f(x)=DNE$

Please log in or register to add a comment.