Hello there. To solve this question, we'll have to remember some properties about mean average, standard deviation and z-score.
In order to determine the cut-off mark the committee should use for this case, in which the students have a mean average of 85 with a standard deviation of 6.
To be in the top 20%, the z-score has to be greater than or equal to 80%, or
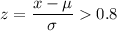
First, we use a z-score table to determine the area to the left of the curve
If the area to the left is bigger than 0.8, the z-score that yields this area is between 0.84 and 0.85
Now, we take the difference
0.85 - 0.84 = 0.01
And the area to the left in each case is, respectively
0.79955 and 0.80234
Taking the difference once again, we get
0.00279
Now we take the difference between the area we want and the area to the left of 0.84, that is
0.8 - 0.79955 = 0.00045
And take the ratio between x, that is the cut off mark and the difference 0.01.
This must be equal to the ratio between the difference of the areas we found:
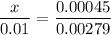
Solving this equation, by multiplying both sides of the equation by 0.01, we get

We add this to the z-score we've found earlier
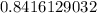
Using the formula in the beginning, we finally solve for x
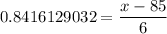
Multiply both sides by 6

Add 85 on both sides of the equation

Hence the cut-off mark is 90 and it is the answer contained in the option b).