Question

The student came to the conclusion that the system has infinitely many solutions, which is not correct. Describe the error the error with the student work being shown.Original Problem:7+5=14+8=21Student Work:Step 1: +8=21=21−8Step 2: (21−8)+8=2121=21Solution: Infinitely Many Solutions

Answer 1

`\begin{gathered} ((7)/(51),(133)/(51)) \\ \end{gathered}`

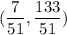
You cannot isolate a variable and then plugin into the same equation, that's why the student got a mistake solution. The system has one solution.

Explanation:

To determine if the system has a solution, solve the system using any method, in this case, let's use the substitution method:

`\begin{gathered} 7x+5y=14\text{ (1)} \\ x+8y=21\text{ (2)} \end{gathered}`

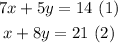
This method consists of isolating one of the variables and substitute it into the other equation:

Isolate x in equation (2)

`\begin{gathered} x=21-8y \\ \end{gathered}`

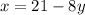
Now, plug this expression in equation (1):

`\begin{gathered} 7(21-8y)+5y=14 \\ 147-56y+5y=14 \\ 147-51y=14 \\ 147-14=51y \\ y=(133)/(51) \end{gathered}`

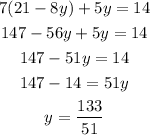
Knowing the solution for y, substitute it into equation (1) to find x:

`\begin{gathered} x=21-8((133)/(51)) \\ x=(7)/(51) \end{gathered}`

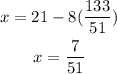
You cannot isolate a variable and then plugin into the same equation, that's why the student got a mistake solution. The system has one solution.