Part a) Springs
For the first part, the instructions say that you should plot the force on the spring versus the extension. From Hooke's Law, we know that:
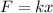
Where F is the force applied by a spring with constant k that is extended a distance x from its equilibrium position.
To find the force applied by the spring, multiply the hanging mass by the acceleration of gravity. Create a table showing force vs. extension. Using the vertical axis for the force F, plot the force on the spring versus the extension. Next, draw a straight line that describes the data points and calculate its slope.
For the second part, create a table where a column for the square root of the mass is included and plot the period versus the square root of the mass. We know that:
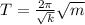
The slope of the period vs. square root of mass corresponds to the factor 2π/√k, from which the constant k can be calculated.
Part b) PendulumFirst, create a table with a column where you calculate the square root of the length. Use the data from that column as the x-axis on your period vs square root of length graph. For a pendulum, we know that:
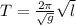
From which we can identify that the slope corresponds to the factor2π/√g, from which the value of g can be calculated.