Question

I need some who is knowledgeable and fast at trigonometry

Answer 1

TO FIND X

Given that the triangle is a right-angled triangle, the length of the three sides can be related using the Pythagorean Theorem, given to be:

`c^2=a^2+b^2`

where c is the hypotenuse, and a and b are the other two sides.

From the diagram provided, we have the following parameters:

`\begin{gathered} a=5 \\ b=x \\ c=12 \end{gathered}`

Therefore, we can calculate the value of x by substituting the values into the formula above and solving:

`\begin{gathered} 12^2=5^2+x^2^{} \\ 144=25+x^2 \\ x^2=144-25 \\ x^2=119 \\ x=\sqrt[]{119} \\ x=10.91 \end{gathered}`

The measure of x is 10.91.

TO FIND θ

We can use the Cosine Trigonometric Ratio to calculate the measure of θ, given to be:

`\cos \theta=\frac{\text{adj}}{\text{hyp}}`

From the diagram provided, we have:

`\begin{gathered} hyp=12 \\ adj=5 \end{gathered}`

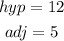
Therefore, we have:

`\begin{gathered} \cos \theta=(5)/(12) \\ \theta=\cos ^(-1)((5)/(12)) \\ \theta=65.38\degree \end{gathered}`

The measure of θ is 65.38°.