Answer 11 :-
We have,
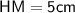
- In square all sides of squares are equal
The perimeter of square
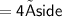
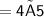
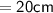
Thus, The perimeter of square is 20 cm
Hence, Option C is correct .
Answer 12 :-
We have,
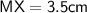
- In square, diagonals are equal and bisect each other at 90°
Here,
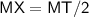
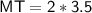
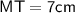
Thus, The MT is 7cm long
Hence, Option C is correct .
Answer 13 :-
We have to find the measure of Angle MAT
- All angles of square are 90° each
From above
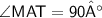
Thus, Angle MAT is 90°
Hence, Option B is correct .
Answer 14 :-
We know that,
- All the angles of square are equal and 90° each
Therefore,
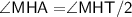
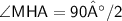
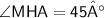
Thus, Angle MHA is 45°
Hence, Option A is correct
Answer 15 :-
Refer the above attachment for solution
Hence, Option A is correct
Answer 16 :-
Both a and b
- The median of isosceles trapezoid is parallel to the base
- The diagonals are congruent
Hence, Option C is correct
Answer 17 :-
In rhombus PALM,
- All sides and opposite angles are equal
Let O be the midpoint of Rhombus PALM
In ΔOLM, By using Angle sum property :-
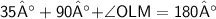
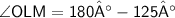
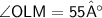
Now,
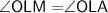
- OL is the bisector of diagonal AM
Therefore,
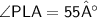
Thus, Angle PLA is 55° .
Hence, Option C is correct