Answer: B
The margin of error is equal to 20
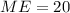
Step-by-step explanation:
Given that the 80% confidence interval is found to be;
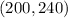
The width of the interval is;
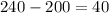
The margin of error is always half the width, so the margin of error is;
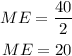
Therefore, the margin of error is equal to 20