Question

Which function has a greater rate of change?Function A:х1.52.53.54.55.5-5051015yFunction B:y = -4.5x + 15and function B has a rate of change ofso Functionhas aFunction Ahas a rate of change ofgreater rate of change.

Answer 1

From the statement of the problem, we have:

• The function A, given by a table of values of x and y,

,

• The function B, given by an equation.

1) For function A, we see that as x increases, the value of y also increases. We also see that the rate of change is constant, given by:

`m_A=(\Delta y)/(\Delta x)=(0-(-5))/(2.5-1.5)=5`

2) For function B, we have the equation:

`y=-4.5x+15.`

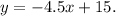
The rate of change of the function is the slope of the line, which is the number that multiplies the variable x. So its rate of change is:

`m_B=-4.5`

Considering the magnitude of the range of changes, we see that:

`\begin{gathered} |m_A|>|m_B| \\ 5>4.5 \end{gathered}`

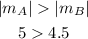
So we conclude that the rate of change of function A is greater than the rate of change of function B.

Answer

Function A has a rate of change of 5 and function B has a rate of change of -4.5, so Function A has a greater rate of change.