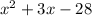Question

Hi I need help with the following: no pictures included Find the polynomial whose solutions are 4 and -7A. Write the polynomial in factored form:B. Write the polynomial in expanded form:I have no idea how to do this or where to began. I am learning factoring in algebra . Please help guide me to understand each step

Answer 1

We have the solutions x = 4 and x = -7, so

A. polynomial in factored form:

Equal the expression to zero, this is:

`\begin{gathered} x-4=4-4 \\ x-4=0 \end{gathered}`

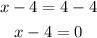
And

`\begin{gathered} x+7=-7+7 \\ x+7=0 \end{gathered}`

Therefore: factor 1 is (x - 4)

factor 2 is (x + 7)

Then we express the polynomial, This is by multiplying the factors

`(x-4)(x+7)`

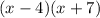
Answer: (x-4)(x+7)

B. Write the polynomial in expanded form:

To find we multiply the two factors

`(x-4)(x+7)`

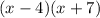
we apply the distributive property

`x\cdot x+x\cdot7-4\cdot x-4\cdot7`

Simplify

`x^2+7x-4x-28`

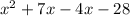
Add 7x - 4x

`x^2+3x-28`

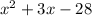
Answer:

`x^2+3x-28`