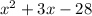We have the solutions x = 4 and x = -7, so
A. polynomial in factored form:
Equal the expression to zero, this is:
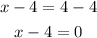
And
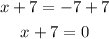
Therefore: factor 1 is (x - 4)
factor 2 is (x + 7)
Then we express the polynomial, This is by multiplying the factors
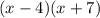
Answer: (x-4)(x+7)
B. Write the polynomial in expanded form:
To find we multiply the two factors
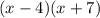
we apply the distributive property
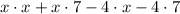
Simplify
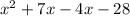
Add 7x - 4x
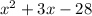
Answer: