y = 6x - 18
STEP - BY - STEP EXPLANATION
What to find?
• The derivative of y.
,
• The value of y when x=3
,
• The value of the intercept c.
,
• The equation of tangent to the curve.
Given:
x = 3
y = In(x² - 8)
To find the equation of the tangent to the curve at x=3, we need to follow the steps below:
Step 1
Find the derivative of y.
Given that y is an implicit function, we will differentiate using the implicit rule.
That is;
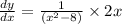
Hence,
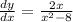
Step 2
Find the value of the derivative in step two at x=3
We can obtain this by substituting x=3 in the above.
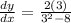
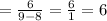
Hence, dy/dx = 6
This implies that slope (m) = 6.
Step 3.
Obtain the value of y at x=3 by substituting x=3 into the original equation and the solving for y.
That is;
y = In(3² - 8)
= In( 9 - 8)
= In (1)
= 0
Hence, y=0 at x=3
Step 4
Obtain the y-intercept (c) by substituting m=6, y=0 and x=3 into y=mx + c
y=mx+c
0 = 6(3) + c
Step 5
Solve for c.
0= 18 + c
Subtract 18 from both-side of the equation.
-18 = c
Hence, c =-18
Step 6
Determine the equation by substituting m= 6 and c=-18 into y=mx + c
y = 6x - 18
Therefore, the equation of the tangent to the curve at the point where x = 3 is y = 6x - 18