In order to find the quadratic equation, let's use the vertex form below:

Where the vertex is located at (h, k).
So, if the vertex is (h, k) = (-4, 2) and using the point (x, y) = (-4, 0), we have:

Since the final statement is false, it's not possible to have a quadratic function with vertex (-4, 2) and with the point (-4, 0).
If we use the point (4, 0) instead, we would have:
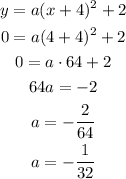
So the equation in this case would be:
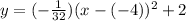
The empty spaces would be filled with the values -1/32, -4 and 2.