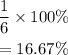Question

6. A basket contains 10 pieces of fruit: 3 apples, 5 oranges, and 2 bananas. When someone chooses a piece of fruit they must eat that fruit and will not put it back. What is the probability that Kala will take an apple and Bradley will take an orange?

Answer 1

The probability that Kala will take an apple and Bradley will take an orange is:

`\begin{gathered} (1)/(6) \\ or \\ 16.67\text{\%} \end{gathered}`

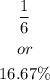
Step-by-step explanation:

We want to find the probability that Kala will take an apple and Bradley will take an orange.

Given:

`\begin{gathered} \text{Total number of fruits = 10} \\ A\text{pples =3} \\ \text{Oranges = 5} \\ \text{Bananas = 2} \end{gathered}`

Since there are no replacament, the probability that Kala picks apple is;

`P_1=(3)/(10)`

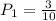
The probability that Bradley will take an orange is;

`P_2=(5)/(9)`

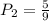
The probability that Kala will take an apple and Bradley will take an orange will be;

`\begin{gathered} P=P_1* P_2 \\ P=(3)/(10)*(5)/(9) \\ P=(15)/(90)=(1)/(6) \end{gathered}`

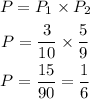
Therefore, the probability that Kala will take an apple and Bradley will take an orange is:

`(1)/(6)`

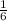
As a percent the probability will be;

`\begin{gathered} (1)/(6)*100\text{\%} \\ =16.67\text{\%} \end{gathered}`