Let 't' be the time at which Andre catches up with Morgan.
We know by definition of distance that:
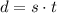
where 's' is the speed and 't' is the time.
In this case, the distance that Morgan travels in time t is:
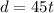
Since Andre starts 2 hours late, we have that in his case, the expression would be:
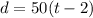
Equating both expressions and solving for t, we get the following:
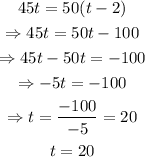
therefore, Morgan would have driven for 20 hours before Andre catches up to him