7) We rearrange the second equation to compare it to the first one:
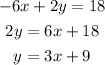
The slopes are m1=1/3 and m2=3. They are not equal, nor negative reciprocals, so they are not parallel nor perpendicular. As they don't have the same slope, they will intersect.
Answer: Intersecting but not perpendicular.
8)
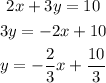
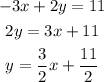
The slopes are negative reciprocals:
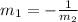
As the slopes are negative reciprocals, both lines are perpendicular.
Answer: Perpendicular.