Let 'x' and 'y' be the cost of one rose bush and one bunch of ornamental grass.
Given that Castel paid $69 for 5 rose bushes and 8 bunches of grass,
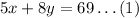
Also, given that Sumalee paid $42 for 2 rose bushed and 8 bunches of grass,
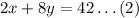
Now that we have two equations and two variables. These can be solved using the Elimination Method.
Subtract equation (2) from (1) as follows,
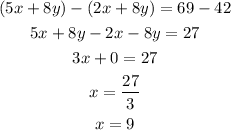
Substitute this value in (1) and obtain the corresponding y-value,
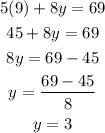
So the simultaneous solution is obtained as,
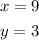
Thus, the cost of one rose bush is $9 and the cost of one bunch of ornamental grass is $3.