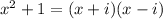The given expression is
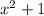
We can not factorize this expression bt the normal factorizing ways
Because it is a binomial with + as a middle sign can not be distributed into 2 factors
Then there is no factorizing for the given binomial
If the sign between the two terms is (-), then we can factorize it into two same factors with different middle sign
We can use the complex numbers to factorize it
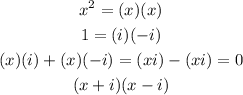
Then the factors are (x + i) and (x - i)