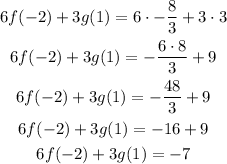First part
To find the value of f(-2), we replace x = -2 into the second piece of the function. Then, we operate.

Second part
To find the value of g(1), we replace x = 1 into the first piece of the function. Then, we operate.
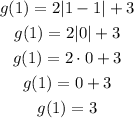
Finally, we find the value of the given expression: