Given the equations
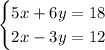
First, she multiplied the second equation by 6:
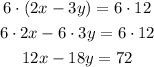
You have to determine the factor to multiply the equation 5x+6y=18 to be able to add both equations and eliminate one of the variables.
To do so, compare the coefficients of the like terms:
5x and 12x, "12" is not a multiple of 5, so there is no factor that when multiplied by 5x will give 12x as a product.
6y and 18y, 18 is a multiple of 6, if you multiply 6y by 3 the product will be 18y.
So, the factor you have to use to multiply the equation and eliminate one variable is 3.