2ab + c²
(a+b)² and a² + 2ab + b²
2ab
1) Examining that picture, we can state the following about that:
The shaded triangles area:
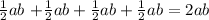
Note that the area of the triangle is 1/2 the product of the base by its height.
The area of that white inner square is given by c² since the Area of a square is equal to the side length raised to the 2nd powe.
2) Then
The expression 2ab + c² represents the area...
The equivalent expressions (a+b)² and a² + 2ab + b² use the length of the figure (a square) raised to the 2nd power. As explained above.
For the last statement let's calculate it:
2ab + c² = (a+b)²
a² +2ab + b² = 2ab +c² Subtracting 2ab
a² +b² = c²
3) Hence, the answers are:
2ab + c²
(a+b)² and a² + 2ab + b²
2ab