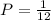Question

A grocer has a bag of fruit containing 3 apples, 2 oranges, and 4 pears. The grocer randomly chooses two pieces of fruit from the bag without looking. What is the probability that the grocer chooses two apples?

Answer 1

The probability that the grocer chooses two apples is;

`P=(1)/(12)`

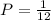
Step-by-step explanation:

Given that;

A grocer has a bag of fruit containing 3 apples, 2 oranges, and 4 pears.

The total number of fruits is;

`\begin{gathered} \text{Apples = 3} \\ \text{Orange = 2} \\ \text{Pears = 4} \\ \text{Total = 3+2+4= 9} \end{gathered}`

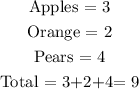
Assuming that the grocer did not replace the fruit after picking, the probability of Picking two apples is;

`P=P_1* P_2`

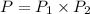
For the first pick;

`\begin{gathered} P_1=\frac{\text{ number of apple}}{\text{ total number of fruits}}=(3)/(9) \\ P_1=(1)/(3) \end{gathered}`

For the second pick, the number of apple and the total number of fruits would have reduced by 1;

`\begin{gathered} P_2=(2)/(8) \\ P_2=(1)/(4) \end{gathered}`

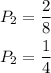
The overall probability is;

`\begin{gathered} P=(1)/(3)*(1)/(4) \\ P=(1)/(12) \end{gathered}`

Therefore, the probability that the grocer chooses two apples is;

`P=(1)/(12)`