We are given Zak's laps jogged along with the minutes elapsed.
If the equation of a line is:
m = kx + b
Where m is the number of minutes.
k is the slope of the line
x is the Laps
b is the y-intercept (or where the line crosses the y-axis)
In order to get the equation of the relationship between Laps (x) and Minutes (m),
we need to calculate the slope k and intercept b.
The formulas for doing these are given below:

The formula for intercept (b) is;
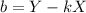
where Y and X are the averages of m and x values from the table.

In order to be tidy and quick, a table is used to solve.
This table is shown in the image below:
Therefore, we can now calculate slope (m):

Now that we have slope (k) = 12, we can get the intercept b
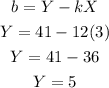
Therefore, the equation is:
m = 12x + 5