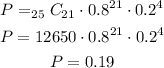Question

At Community Hospital, the nursing staff is large enough so that 80% of the time a nurse canrespond to a room call within three minutes. Last night there were 25 room calls. Find theprobability that nurses responded to 21 of the calls within three minutes.

Answer 1

This situation can be modeled by the binomial distribution, because there are two outcomes: a nurse can respond or a nurse cannot respond. The probability, p, that a nurse can respond is 0.8 (or 80%), the probability, q, that a nurse cannot respond is 0.2 (= 1 - 0.8). In 25 trials, we need that in 21 of them a nurse can respond.

The binomial distribution formula is:

`P=_nC^{}_xp^xq^(n-x)`

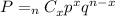
where xCn means number of combinations, n is the number of trials, x is number of times for a specific outcome within n trials, p is the probability of succes, and q is the probability of failure.

Substituting with n = 25, x = 21, p = 0.8 and q = 0.2, we get:

`\begin{gathered} P=_(25)C_(21)\cdot0.8^(21)\cdot0.2^4 \\ P=12650\cdot0.8^(21)\cdot0.2^4 \\ P=0.19 \end{gathered}`