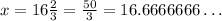To solve this equation, we can proceed as follows:
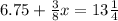
1. Subtract 6.75 to both sides of the equation:
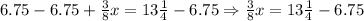
We can solve the right part of the equation using fractions as follows:
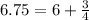
We also know that
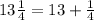
Then, we have:
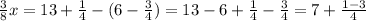
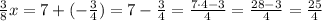
Now, the equation is:
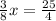
We need to multiply by 8/3 to both sides to solve for x as follows:
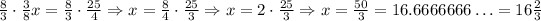
Therefore, the value for x is equal to: