SOLUTION
Define a variable for the unkwons

Then
6 dozen of doughnuts and 2 dozen of croissant cost $42, is written as
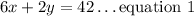
Similarly
$40 for 2 dozen of doughnuts and 5 dozen of croissant is witten as
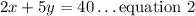
Applying Elimination to solve the two system of equation, we have
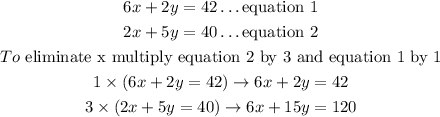
Then, subtract the equation obtained above
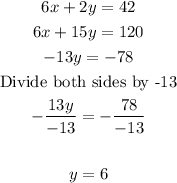
Hence Y=6
Then you Eliminate Y from eqaution 1 an d 2 by
Multiplying equation 1 by 5 and equation 2 by 2
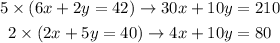
The sunbtract the equation obtained
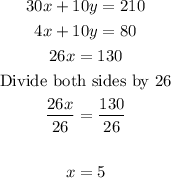
Hence X=5
Therefore
A Dozen of doughnuts cost $5
A Dozen of Croisant cost $6