ANSWER
x = -2 and x = 6
Step-by-step explanation
The rate of change of the function is the derivative of the function.
In this case, we have the function,
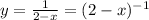
Using the chain rule,
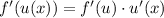
In this case, u = 2 - x and f(u) is u⁻¹,
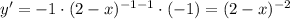
The rate of change is,
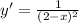
We have to find for which values of x, y' = 1/16. Thus, we have to solve the equation,
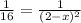
Raise both sides to the exponent -1 - i.e. flip both sides of the equation,
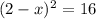
Take the square root of both sides - remember that the square root has a negative and a positive result,
![\begin{gathered} \sqrt[]{(2-x)^2}=\pm\sqrt[]{16} \\ \\ 2-x=\pm4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/qxbxm92zn0ycyo7gqmtggmblbb8m000trp.png)
Subtract 2 from both sides,

And multiply both sides by -1,
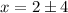
Hence, the values of x for which the rate of change of y with respect to x is equal to 1/16 are x = -2 and x = 6