Let x and y be the two numbers we are trying to find.
'One number is 9 more 3 times another' is equivalent to x=9+3y
'Their product is 9 more than 3 times their sum' is equivalent to xy=9+3(x+y)
We have two equations and two unknowns; therefore, we can solve the problem
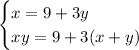
Solve it as shown below
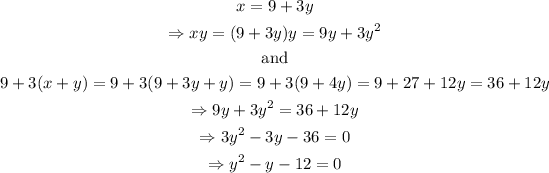
Solve the quadratic equation
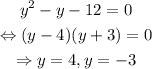
Finally,
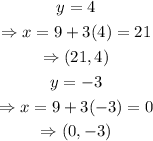
The solutions are (21,4) and (0,-3)