Question

A string 0.50 m long is stretched under a tension of 2.0 x 102 N and its fundamental frequency is 400 Hz. If the length if the string is shortened to 0.35 m and the tension is increased to 4.0 x 102 N, what is the new fundamental frequency?

Answer 1

Given,

The initial length of the string, L₁=0.50 m

The tension on the string, T₁=2.0×10² N

The initial fundamental frequency of the string, f₁=400 Hz

The length of the string after it was shortened, L₂=0.35 m

The increased tension on the string, T₂=4.0×10² N

The fundamental frequency of the string before it was shortened is given by,

`f_1=\frac{\sqrt[]{(T_1)/(\mu)}}{2L_1}`

Where μ is the mass per unit length of the string.

On rearranging the above equation,

`\begin{gathered} 4L^2_1f^2_1=(T_1)/(\mu) \\ \Rightarrow\mu=(T_1)/(4L^2_1f^2_1) \end{gathered}`

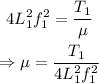
On substituting the known values,

`\begin{gathered} \mu=(2.0*10^2)/(4*0.50^2*400^2) \\ =1.25*10^(-3)\text{ kg/m} \end{gathered}`

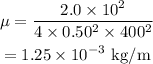
The fundamental frequency after the string was shortened is given by,

`f_2=\frac{\sqrt[]{(T_2)/(\mu)}}{2L_2}`

On substituting the known values,

`\begin{gathered} f_2=\frac{\sqrt[]{(4*10^2)/(1.25*10^(-3))}}{2*0.35} \\ =808.1\text{ Hz} \end{gathered}`

Thus the fundamental frequency after the string is shortened and the tension is increased is 808.1 Hz