Question

the sum of the digits of a two-digit number is 11. If the digits are reserved the new number is 27 more than the original number. Find the original number.

Answer 1

Consider the digits of two digit number as x and y.

It is given that sum of the two digit number if 11.

Then,

`x+y=11\text{ ..}...(1)`

If the numbers are reversed, new number is 27 more than the original number.

Then the reversed number can be written as 10y and x.

Now equate the two numbers.

`\begin{gathered} 10y+x=(10x+y)+27 \\ 10y+x-10x-y=27 \\ -9x+9y=27\ldots\ldots.(2) \end{gathered}`

Solve equation (1) and (2) by multiplying equation (1) by -9.

`\begin{gathered} -9x-9y=-99 \\ -9x+9y=27 \\ -18x=-72 \\ x=(72)/(18) \\ x=4 \end{gathered}`

Now, substitute the value of x in equation (1) to find the value of y.

`\begin{gathered} 4+y=11 \\ y=11-4 \\ y=7 \end{gathered}`

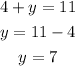
Thus, the value of x is 4 and the value of y is 7.

Hence, the original number of 47.