ANSWER
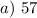
Step-by-step explanation
We want to find the angle at which the range for the projectiles will be the same.
The range for a projectile is given by:
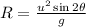
where u = initial velocity
θ = angle of the projectile
g = acceleration due to gravity
For a projectile to have the same range as one with an angle of 33° (given that other values are constant), the value of sin(2θ) must be equal for both projectiles.
Let us find the value of sin(2(33°)):
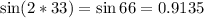
Let us find the same for the angles in the options:
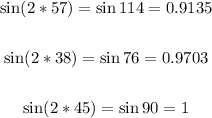
As we can see, the angle that will result in the same range as 33° is 57°.
The answer is option a.