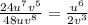Answer
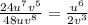
Solution
- The question asks us to simplify the following expression:
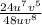
- In order to solve this, we need to know some laws of exponents to help us with the solution. The relevant laws of exponents for this question are given below:
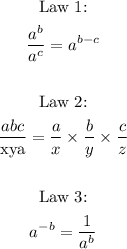
- Now that we have the laws of exponents we require, we can proceed to solve the question.
- This is done below:

Final Answer