Question

E. O 5.945 m/s7. An object of mass 7 kg going to the right witha speed of 9 m/s collides with a(n) 12 kg object going tothe left with a speed of 20 m/s. If the collisionis completely elastic, calculate the speed of the 12 kgobject after collision. (1 point)A. O 0.972 m/sB. 02.028 m/sC. O 1.794 m/sD. O 1.368 m/sE. O 2.38 m/s2

Answer 1

Since the collision is an elastic one the momentum and kinetic energy of the system is conserved; this means that:

`\begin{gathered} m_1v_1+m_2v_2=m_1u_1+m_2u_2 \\ (1)/(2)m_1v_1^2+(1)/(2)m_2v_2^2=(1)/(2)m_1u_1^2+(1)/(2)m_2u_2^2 \end{gathered}`

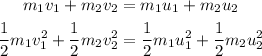
In this case we have:

`\begin{gathered} m_1=7 \\ v_1=9 \\ m_2=12 \\ v_2=-20\text{ Since the 12 kg object is moving to the left} \end{gathered}`

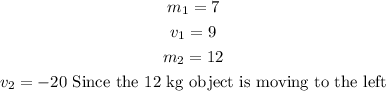
Plugging these values in the momentum equation we have:

`\begin{gathered} 7u_1+12u_2=(7)(9)+(12)(-20) \\ 7u_1+12u_2=-177 \end{gathered}`

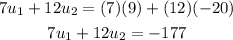
And plugging them in the energy equation:

`\begin{gathered} (1)/(2)(7)u_1^2+(1)/(2)(12)u_2^2=(1)/(2)(7)(9)^2+(1)/(2)(12)(-20)^2 \\ 7u_1^2+12u_2^2=5367 \end{gathered}`

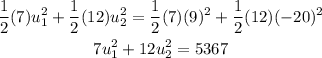
Then we have the system of equations:

`\begin{gathered} 7u_(1)+12u_(2)=-177 \\ 7u_1^2+12u_2^2=5367 \end{gathered}`

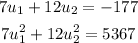
Solving the first equation for u1 we have:

`u_1=-(12u_2+177)/(7)`

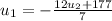
Plugging these in the second equation we have:

`\begin{gathered} 7(-(12u_2+177)/(7))^2+12u_2^2=5367 \\ (1)/(7)(144u_2^2+4248u_2+31329)+12u_2^2=5367 \\ 144u_2^2+4248u_2+31329+84u_2^2=37569 \\ 228u_2^2+4248u_2-6240=0 \\ \text{ Using the quadratic formula we have:} \\ u_2=(-4248\pm√(4248^2-4(228)(-6240)))/(2(228)) \\ u_2=(-4248\pm4872)/(456) \\ \text{ Then} \\ u_2=(-4248+4872)/(456)=1.368 \\ \text{ or} \\ u_2=(-4248-4872)/(456)=-20 \end{gathered}`

The negative solution is the velocity when the objects collide then we need to choose the other solution.

Therefore, the velocity of the 12 kg object after they collide is 1.368 m/s