Question

(x-2)2+(y-5)2=16 moved up 3 units and 1 to left where is the center resulting circle whsts the radius and equation

Answer 1

Given:

The equation of a circle is,

`(x-2)^2+(y-5)^2=16\text{ . . . .(1)}`

The circle is moved 3 units up and 1 unit left.

The objective is to find the center of the circle, the radius of the circle, and the final equation.

Step-by-step explanation:

The general equation of a circle is,

`(x-h)^2+(y-k)^2=r^2\text{ . . . . .(2)}`

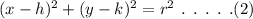
Here, (h,k) represents the center of the circle and r represents the radius of the circle.

The given equation can be written as,

`(x-2)^2+(y-5)^2=4^2\text{ . . . . .(3)}`

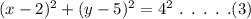
By comparing equation (2) and equation (3),

`\begin{gathered} (h,k)=(2,5) \\ r=4 \end{gathered}`

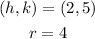
To find the center of new the circle:

It is given that the circle is moved 3 units up (y-axis) and 1 unit to left (x-axis).

Then, the center of the circle can be written as,

`\begin{gathered} (h^(\prime),k^(\prime))=(h-1,y+3) \\ (h^(\prime),k^(\prime))=\mleft(2-1,5+3\mright) \\ (h^(\prime),k^(\prime))=(1,8) \end{gathered}`

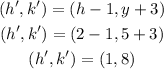
Thus, the center of the new circle is (h', k') = (1,8).

The radius of the circle will be the same as r = 4 since only the position of the circle is changed.

To find the equation of the new circle:

The equation of the new circle can be calculated by substituting the obtained values of the new circle in equation (1).

`\begin{gathered} (x-h^(\prime))+(y-k^(\prime))=r^2 \\ (x-1)^2+(y-8)^2=4^2 \\ (x-1)^2+(y-8)^2=16 \end{gathered}`

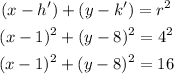
Hence, the center of the new circle is (1,8), the radius of the new circle is 4, and the equation of the new circle is (x-1)²+(y-8)² = 16.