Answer
(a)
![f^(-1)(x)=\sqrt[]{x+13},\text{ }x\ge-13](https://img.qammunity.org/2023/formulas/mathematics/college/jg8bi5dlx2zyzczrdp6mhkl0iipn9vhr1x.png)
(c) The domain and range of f(x) are:
Domain is [0, ∞) and the range is [-13, ∞)
The domain and range of f⁻¹(x) are:
Domain is [-13, ∞) and the range is [0, ∞)
Step-by-step explanation
Given function:
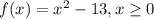
(a) To find f⁻¹(x)
Let y = f(x)
This implies
![\begin{gathered} y=x^2-13 \\ y+13=x^2 \\ x^2=y+13 \\ x=\sqrt[]{y+13} \\ \text{Note that x }=f^(-1)(y) \\ f^(-1)(y)=\sqrt[]{y+13} \\ \therefore f^(-1)(x)=\sqrt[]{x+13},\text{ }x\ge-13 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/mp333ftryccwsje4wzj6mb9tlpcc5vr460.png)
(c) The domain and range of f(x) are:
Domain is [0, ∞) and the range is [-13, ∞)
The domain and range of f⁻¹(x) are:
Domain is [-13, ∞) and the range is [0, ∞)