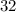Step-by-step explanation:
Consider the following right isosceles triangle with a hypotenuse of 8√2:
Remember that an isosceles triangle is a triangle that has two sides of equal length. In this case. the sides other than the hypotenuse have the same measure.
Now, applying the Pythagorean theorem we obtain the following equation:
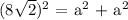
or
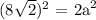
or
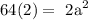
this is equivalent to:
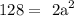
then:
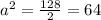
solving for a:
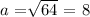
Then, the area A of the given right isosceles triangle would be:
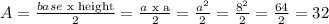
then, we can conclude that the correct answer is:
Answer: