Question

If a ball is thrown upward at 49 meters per second from the top of a building that is 30 meters high, the height of the ball can be modeled by S=30+49t−4.9t2, where t is the number of seconds after the ball is thrown.Answer parts a through c.

Answer 1

The height of the ball can be modeled by the equation:

`S=30+49t-4.9t^2`

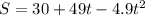
Where t is the time (seconds) after the ball is thrown.

The general form of the quadratic function is given by:

`f(x)=ax^2+bx+c`

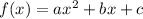
If you take a look, the equation can be written in this form:

`S=-4.9t^2+49t+30`

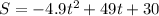
Where a=-4.9, b=49 and c=30.

a. The vertex of the quadratic function is given by (h,k), where:

`\begin{gathered} h=-(b)/(2a) \\ k=f(h) \end{gathered}`

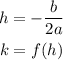
By finding h, you will obtain the t-coordinate of the vertex:

`\begin{gathered} h=-(49)/(2(-4.9))=-(49)/(-9.8) \\ h=5 \end{gathered}`

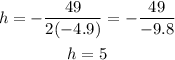
Thus, the t-coordinate of this quadratic function is t=5.

The S-coordinate of this quadratic function corresponds to the k-coordinate of the vertex: k=f(h). Then, let's evaluate the function in t=5:

`\begin{gathered} f(5)=-4.9(5)^2+49(5)+30 \\ f(5)=-4.9*25+49*5+30 \\ f(5)=-122.5+245+30 \\ f(5)=152.5 \end{gathered}`

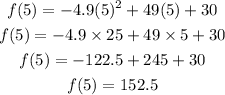
Thus, the S-coordinate of this quadratic function is S=152.5.

b. The vertex coordinates are (t, S)= (5, 152.5). It means that the ball reaches its maximum height (S) of 152.5 meters in a time (t) of 5 seconds. The answer is option D.

c. The function will be increasing until the ball reaches its maximum height (until the vertex), thus, it is increasing until t=5 seconds. After this time, the ball will start to fall. The answer is option A.