Question

A positive integer is 5 less than another. If the sum of the reciprocal of a smaller and twice the reciprocal of the larger is 11/14, then find the two integers.

Answer 1

Given:

a.) A positive integer is 5 less than another.

b.) The sum of the reciprocal of a smaller and twice the reciprocal of the larger is 11/14.

From the given, let's generate the equation each of the givens represents.

Let,

x = The lesser number

y = The larger number

a.) A positive integer is 5 less than another.

`\text{ x = y - 5}`

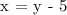
b.) The sum of the reciprocal of a smaller and twice the reciprocal of the larger is 11/14.

`(1)/(x)+2((1)/(y))\text{ = }(11)/(14)`
`(1)/(x)+\text{ }(2)/(y)=(11)/(14)`

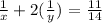
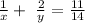
Step 1: Let's substitute x = y - 5 to the other equation to be able to find x.

`(1)/(x)+\text{ }(2)/(y)=(11)/(14)\text{ }\rightarrow(1)/(y-5)+\text{ }(2)/(y)=(11)/(14)`

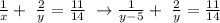
Step 2: Let's simplify the equation, let's transform the two addends into a fraction with a common denominator. The common denominator will be y(y-5). We get,

`(1)/(y-5)+\text{ }(2)/(y)=(11)/(14)\text{ }\rightarrow\text{ }((1)(y))/(y(y-5))\text{ + }((2)(y-5))/(y(y-5))\text{ = }(11)/(14)`
`\frac{y\text{ + 2y - 10}}{y^2-5y}\text{ = }(11)/(14)\text{ }\rightarrow\text{ (14)(}y\text{ + 2y - 10) = (11)(}y^2-5y)`
`14y+28y-140=11y^2\text{ - 55y}`
`42y-140=11y^2\text{ - 55y }\rightarrow11y^2\text{ - 55y - 42y + 140 = 0 }\rightarrow11y^2\text{ -97y + 140 = 0}`

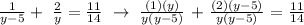
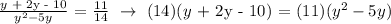
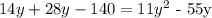
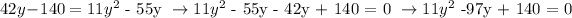
Step 2: Let's find the solution to the quadratic equation.

`\text{y = }\frac{-b\text{ }\pm\text{ }\sqrt[]{b^2-4ac}}{2a}`

From the given equation, a = 11, b = -97 and c = 140. Let's plug in the values.

`\text{ y = }\frac{-b\text{ }\pm\text{ }\sqrt[]{b^2-4ac}}{2a}\text{ }\rightarrow\text{ y = }\frac{-(-97)\pm\text{ }\sqrt[]{(-97)^2-4(11)(140)}}{2(11)}`
`\text{ y = }\frac{97\pm\text{ }\sqrt[]{9,409^{}-6,160}}{22}\text{ }\rightarrow\text{ y = }\frac{97\pm\text{ }\sqrt[]{3249}}{22}`
`\text{ y = }\frac{97\text{ }\pm\text{ 57}}{22}`
`y_1\text{ = }\frac{97\text{ + 57}}{22}\text{ = }(154)/(22)\text{ = 7}`
`\text{ y}_2\text{ =}\frac{97\text{ - 57}}{22}=(40)/(22)\text{ = }(20)/(11)`

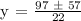
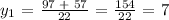
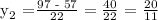
Step 3: Let's substitute 7 and 20/11 to the equation if which among them is real and correct.

a.) At y = 7, x = y - 5 = 7 - 5 = 2

`(1)/(x)+(2)/(y)\text{ = }(11)/(14)\text{ }\rightarrow\text{ }(1)/(2)+(2)/(7)=\text{ }(11)/(14)\text{ }\rightarrow\text{ }(7)/(14)+(4)/(14)\text{ = }(11)/(14)`
`(11)/(14)\text{ = }(11)/(14)`

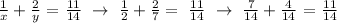
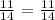
b.) At y = 20/11, x = x - 5 = 20/11 - 5 = 20/11 - 55/11 = -35/11

`(1)/(x)+(2)/(y)\text{ = }(11)/(14)\text{ }\rightarrow\text{ }(1)/(-(35)/(11))+(2)/((20)/(11))=\text{ }(11)/(14)\text{ }\rightarrow\text{ -}(11)/(35)\text{ + }(2(11))/(20)\text{ = }(11)/(14)\text{ }\rightarrow\text{ -}(11)/(35)\text{ + }(22)/(20)\text{ = }(11)/(14)`
`((22)(35))/(700)\text{ - }((11)(20))/(700)=\text{ }(11)/(14)\text{ }\rightarrow\text{ }\frac{770\text{ - 220}}{700}\text{ = }(11)/(14)\text{ }\rightarrow\text{ }(550)/(700)\text{ = }(11)/(14)`
`((550)/(50))/((700)/(50))\text{ = }(11)/(14)\text{ }\rightarrow\text{ }(11)/(14)\text{ = }(11)/(14)`

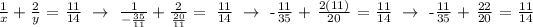
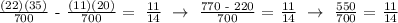
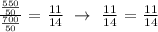
The integers that will satisfy the criteria.

Pair 1: Lesser number = 2 and the Larger number = 7

The second set of pairs is not to be considered integers because it has a concurrent decimal equivalent. A fraction can only be called an integer if it can be simplified into a whole number.