Answer:
• 2x
,
• x-4
,
• x²+4x+16
Explanation:
Given the volume of a rectangular prism:
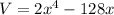
To determine the side lengths, we factor the expression for V.
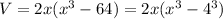
Next, we factorize x³-4³ using the difference of two cubes rule:
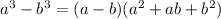
Therefore:
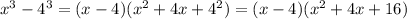
The factored form of V is, therefore:
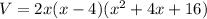
The lengths of the prism's sides are 2x, x-4 and x²+4x+16.