We are given a two-way probability table.
We are asked to find the conditional probability that it was a coupe, given that the selected vehicle was Brand 1.
P(coupe | Brand 1) = ?
Recall that the conditional property is given by
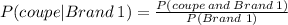
From the given table we see that,
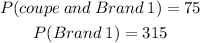
So, the probability is
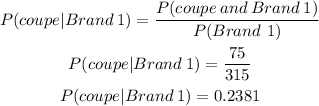
Therefore, the probability that a vehicle was a coupe, given that it was Brand 1, is found to be 0.2381