Question

Due in 10 hours, 51 minutes. Due Thu 06/09/2022 11:59Tickets for a school event were $2.50 for students and $3.00 for parents. If a total of 100 tickets were sold for$272.50, how many student and parent tickets were sold?There werestudent tickets sold andparent tickets sold.

Answer 1

Let x and y be the number of tickets for students and for parents respectively.

Therefore, the two equations mentioned in the question are

`\begin{gathered} x+y=100 \\ 2.5x+3y=272.5 \end{gathered}`

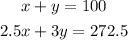
Solve the system of equations as shown below

`\begin{gathered} \Rightarrow x=100-y \\ \Rightarrow2.5(100-y)+3y=272.5 \\ \Rightarrow250+0.5y=272.5 \\ \Rightarrow0.5y=22.5 \\ \Rightarrow y=45 \end{gathered}`

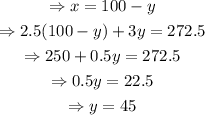
Finding x,

`\begin{gathered} y=45 \\ \Rightarrow x=100-45=55 \end{gathered}`

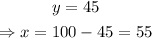
Therefore, there were 55 student tickets sold and 45 parent tickets sold.