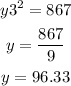Question

Suppose that y varies inversely as the square of x, and that y = 3 when x = 17. What is y when x = 3? Round your answer to two decimal places if necessary.

Answer 1

we know that

If y varies inversely as the square of x

then

the equation is equal to

`yx^2=k`

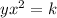
where

k is the contant of proportionality

step 1

Find the constant k

For y=3, x=17

substitute the given values

`\begin{gathered} 3(17^2)=k \\ k=867 \end{gathered}`

we have the equation

`yx^2=867`

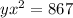
step 2

Find the value of y when the value of x=3

substitute in the equation

`\begin{gathered} y3^2=867 \\ y=(867)/(9) \\ y=96.33 \end{gathered}`