We want to find the points on the curve y = x² + 1 that are closest to the point (0,2).
For any given value x, its correspondent point on the curve will be (x,x² + 1)
The distance between (0,2) and (x,x² + 1) is given by:
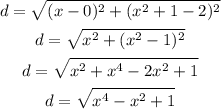
Now, to find the values of x associated to the closest point of (0,2), we must derivate d and find x for d'(x) = 0:
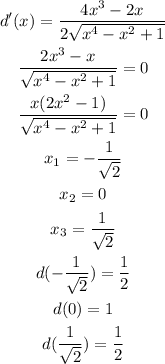
Then we have:
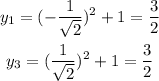
Anser:
(-0.71,1.5), (0.71,1.5)