Question

A boy wants use his slingshot to shoot a water balloon into the air. Hisslingshot has a spring constant of 50 N/m, and he pulls it back 1.5 m beforereleasing the water balloon and launching it into the air. If air resistance canbe ignored and the water balloon has a mass of 1.5 kg, what is theapproximate maximum height that the water balloon can reach? (Recall that g= 9.8 m/s²)O A. 4.6 mB. 0.7 mC. 2.1 mD. 3.8 m

Answer 1

Given:

The mass of the water balloon is,

`m=1.5\text{ kg}`

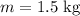
The spring constant is,

`k=50\text{ N/m}`

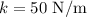
The spring pulls back the slingshot by,

`x=1.5\text{ m}`

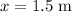
To find:

the

approximate the maximum height that the water balloon can reach

Step-by-step explanation:

The potential energy of the spring converts into the kinetic energy of the balloon and helps it to reach a maximum height.

The potential energy of the spring is,

`\begin{gathered} (1)/(2)kx^2 \\ =(1)/(2)*50*1.5^2 \\ =56.25\text{ J} \end{gathered}`

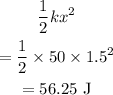
The potential energy of the balloon at the maximum height 'h' is,

`\begin{gathered} mgh \\ =1.5*9.8h \end{gathered}`

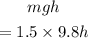
We can write,

`\begin{gathered} 1.5*9.8h=56.25 \\ h=(56.25)/(1.5*9.8) \\ h=3.8\text{ m} \end{gathered}`

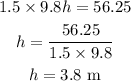
Hence, the water balloon can reach upto 3.8 m.