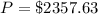To answer this question, we have to use the next formula, which is the continuous compounding interest formula:
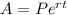
Where:
• A is the accrued amount. In this case, we have A = $5,200.
,
• P is the principal. This is the amount we need to find.
,
• r is the interest rate. In this case, the value is r = 7.91% or 7.91/100.
,
• t is time in years. In this case, t = 10 years.
,
• e is the "e" number (e is approximately 2.71828182846)
Therefore, we have:
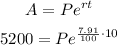
Now, we have to solve the equation by using the inverse function of the natural exponential function, namely, the natural logarithm as follows:
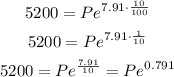
Now, we can see that is not necessary to use the natural logarithm. We have to divide both sides by the resulting exponential value:
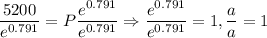
Therefore, we finally have:
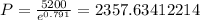
If we round the resulting value to two decimal places, we have that: