Question

Solve the following system of linear equations by substitution and determine whether the system has one solution, no solution, or an infinite number of solutions. If theSystem has one solution, find the solution5x+y=-28- 7x - 4y =8Answer

Answer 1

Given the equation system

`\begin{gathered} 1)5x+y=-28 \\ 2)-7x-4y=8 \end{gathered}`

First, write the first equation for y

`\begin{gathered} 5x+y=-28 \\ y=-28-5x \end{gathered}`

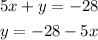
Second, replace the expression in the second equation, that way you'll determine one expression with one unknown

`-7x-4(-28-5x)=8`

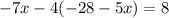
Now you can solve for x

Start solving the multiplication on the parenthesis term by applying the distributive propperty of multiplications

`\begin{gathered} -7x+(-4\cdot-28)+(-4\cdot-5x)=8 \\ -7x+112+20x=8 \end{gathered}`

Order the like terms and simplify

`\begin{gathered} -7x+20x+112=8 \\ 13x+112=8 \end{gathered}`

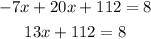
Pass "112" to the other side of the equation by performing the opposite operation, that is to subtract the number from both sides of the equation

`\begin{gathered} 13x=8-112 \\ 13x=-104 \end{gathered}`

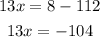
Divide both sides by 13 to reach the value of x

`\begin{gathered} (13x)/(13)=-(104)/(13) \\ x=-8 \end{gathered}`

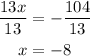
Finally, replace the value of x in the first equation to determine the value of y

`\begin{gathered} y=-28-5x \\ y=-28-5(-8) \\ y=12 \end{gathered}`

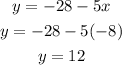
The equation system has one solution for x=-8 and y=12